Création d’un Cube en C# (procédural) : Unity

Bonjour à tou-te-s ! Ici Key en direct du studio de Make Your Game. Le thème du tuto d’aujourd’hui est la génération d’un cube en procédural dans Unity.

Je vous préviens tout de suite, ce tutoriel n’est pas insurmontable, mais si vous voulez pouvoir comprendre et adapter les concepts que nous allons explorer, je vous conseille d’avoir une petite base en programmation.

Pourquoi générer un cube à la main ?

Il est vrai qu’Unity fournit nativement des Mesh, on pourrait simplement utiliser le cube primitif. C’est un avantage et un inconvénient : avoir un volume déjà construit permet de travailler rapidement avec ce dernier, cependant l’agencement interne du Mesh en question n’est pas pensé pour être manipulé de façon intuitive.

Admettons que vous voudriez avoir un contrôle complet sur une texture à appliquer sur votre objet, ou même d’un comportement physique particulier, la façon dont est composé le Mesh de cet objet affectera votre façon de travailler. Si le Mesh de votre GameObject est conçu par vos soins, vous aurez plus de facilité à le manipuler.

Des mathématiques !

Qui dit création d’un cube à la main dans Unity, dit forcément géométrie dans l’espace !

Je vous rassure, vous n’êtes pas obligé d’être ingénieur en maths pour comprendre les notions que l’on va aborder (je ne suis pas moi-même un fin mathématicien), mais ce tutoriel va vous demander d’intégrer des connaissances géométriques à votre culture de développeur/développeuse.

L’API d’Unity offre nativement des volumes géométriques (cube, capsule, sphère etc). Ces formes sont créées à partir d’un Mesh.

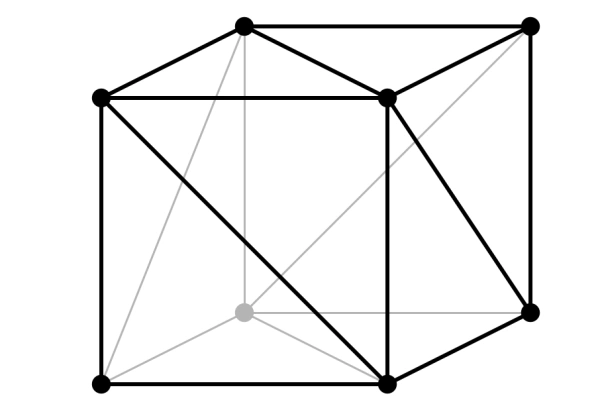
Un Mesh est lui-même composé de triangles délimités par des sommets (vertices). Pour constituer un Mesh, il va falloir : placer les vertices dans un espace en 3D (avec des “Vector3”) ; créer les triangles en retenant l'ordre précis dans lequel les vertices compose chaque triangle.

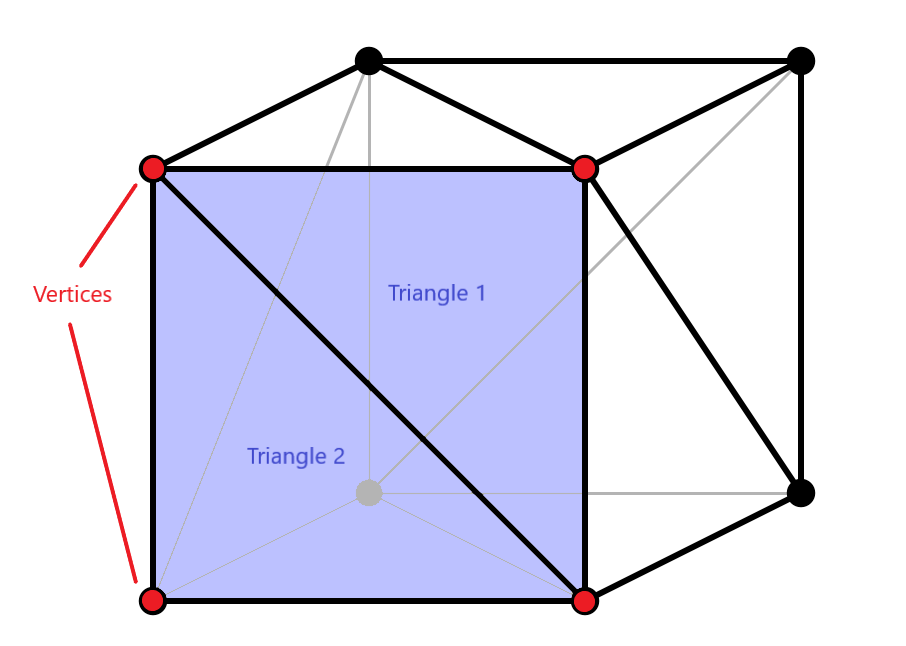L’ordre dans lequel il faudra stocker les vertices composants les triangles est dans le sens des aiguilles d’une montre.

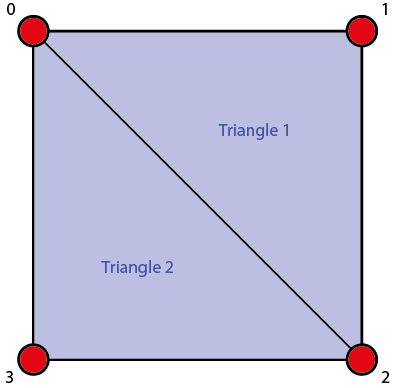Par exemple : admettons que la figure ci-dessus soit l’une des faces de notre cube, il faudrait dans un premier temps stocker dans les vertices 0, 1 et 2 pour composer le triangle 1 ; puis stocker les vertices 0, 2 et 3 pour le triangle 2.

Chaque triangle qui construira notre cube va être construit par 3 vertices : un cube dans la réalité est composé de 8 sommets ; un cube dans Unity est composé de 24 vertices.

Exemple :
1 cube = 6 faces = 12 triangles = 24 vertices
1 face = 2 triangles = 4 vertices
1 triangle = 3 vertices

Cela peut paraître un peu abstrait pour le moment, mais cette notion prendra tout son sens dans la mise en pratique.

Le but de ce tutoriel est de comprendre ces concepts complexes et de les appliquer pour créer objets 3D en C#. Nous aurions pu également constituer d’autres volumes, mais pour le moment, contentons-nous de réussir à créer un cube pour comprendre le principe.

3… 2… 1… Codez !

Mise en place de la scène

Pour la mise en place, rien de très sorcier, ouvrez un nouveau projet Unity, appelez-le comme vous le sentez. Créez un dossier “Script” et un dossier “Material” dans le dossier “Asset”.
Créez un script “CubeGenerator” et placez dans le dossier “Script”.

Puis ajoutez un material dans le dossier dédié. Donnez-lui la couleur que vous voulez pour votre cube, pour ma part, il sera blanc.

Créez ensuite un GameObject vide et associez-lui le script fraîchement créé.

Attribuez au “CubeGenerator” une icône (pour une meilleure visibilité) et une valeur de 2 sur sa position sur l’axe Y comme ci-dessous.

Vous pouvez maintenant ouvrir le script pour passer à la phase de code !

Scripting

Première étape, nous allons déclarer les variables dont nous aurons besoin pour notre générateur de cube.

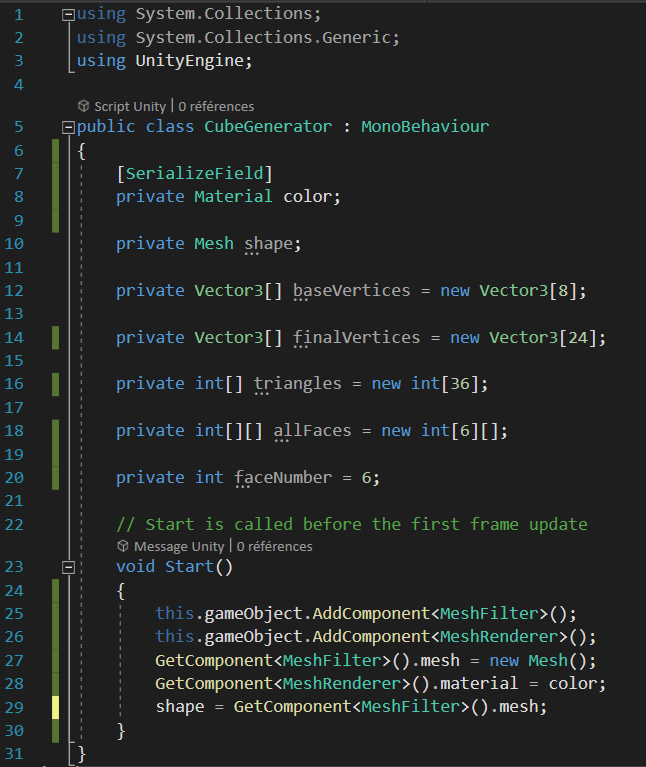
Pour commencer, il faut retirer la méthode “Update()” elle ne nous sera d’aucune utilité ici.
Il faudra ensuite déclarer une variable “color” et “shape” :

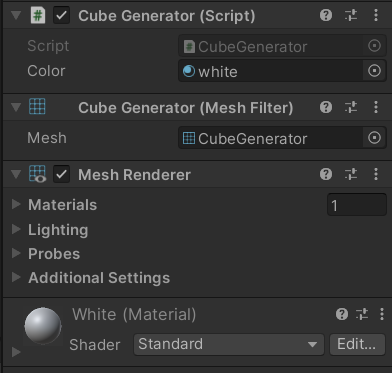
- “shape” va accueillir le Mesh qui sera à générer ; on lui crée le component MeshFilter en ligne 25, on donne ensuite un Mesh vierge (en ligne 27) à notre GameObject vide et on attribue en ligne 29 ce nouveau Mesh à la variable “shape”

- “color” va accueillir le material créé plus tôt ; en ligne 26 on crée un MeshRenderer, puis en ligne 28 on lui attribue notre material

Remarque : N’oubliez surtout pas le MeshRenderer ! Votre cube ne sera pas visible s’il n’a pas de rendu !

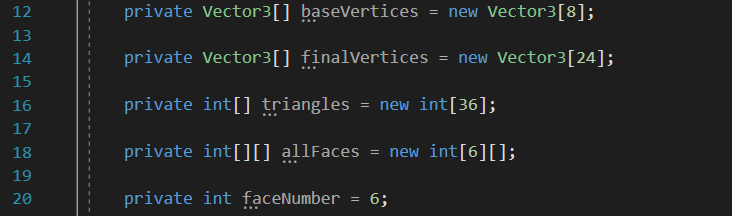
La variable “baseVertices” va stocker les coordonnées (Vector3) des vertices de base, donc les 8 sommets de base d’un cube.

La variable “finalVertices” va stocker les vertices finales. Comme expliqué plus haut, le nombre total de vertices pour un cube (sous Unity) est de 24. Chaque vertex (vertex = vertices au singulier) auront les mêmes coordonnées que celles d’un cube de base. Cette variable va servir à stocker chaque coordonnées des vertices de chaque triangle (donc les 24 attendues) pour les associer au Mesh.

La variable “triangles” va stocker tous les vertices composant chaque triangle du cube. Ces vertices doivent être stockées dans l’ordre explicité plus haut (dans le sens des aiguilles d’une montre, voir l’exemple dans la section “Des mathématiques !”).

Remarque : Il y a effectivement 12 triangles pour constituer un cube, cependant, chaque triangle est composé de 3 vertices qui lui sont propres.
Donc 3 vertices x 12 triangles = 36 vertices à stocker dans la variable “triangles”.

La variable “allFaces” va stocker un un tableau à deux dimensions. Chaque tableau stocké dans cette variable va contenir les indexes des “baseVertices” composant chaque face du cube.
Exemple :

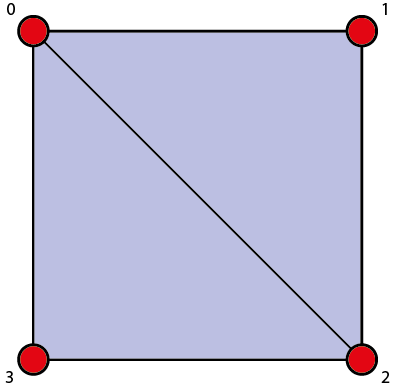
Admettons que la figure ci-dessus est la 1ère face de notre cube.
Cette face est composée des vertices de base (donc les coordonnées Vector3 stockées dans la variable “baseVertices”).
La variable “allFaces” va enregistrer dans chacun de ses tableaux, les indices du tableaux “baseVertices” (permettant d'accéder au coordonnées Vector3) correspondants aux sommets composant chaque face du cube. Ces coordonnées seront utilisées pour placer les vertices propres aux triangles.

Remarque : Si l’explication a été claire, vous devez avoir compris que chaque sommet du cube aura 3 vertices placées aux mêmes coordonnées, chacune correspondant aux triangles qui se rejoignent en ce sommet.

Et enfin, la variable “faceNumber” stocke le nombre de faces, cela va nous permettre d’automatiser le remplissage des tableaux.

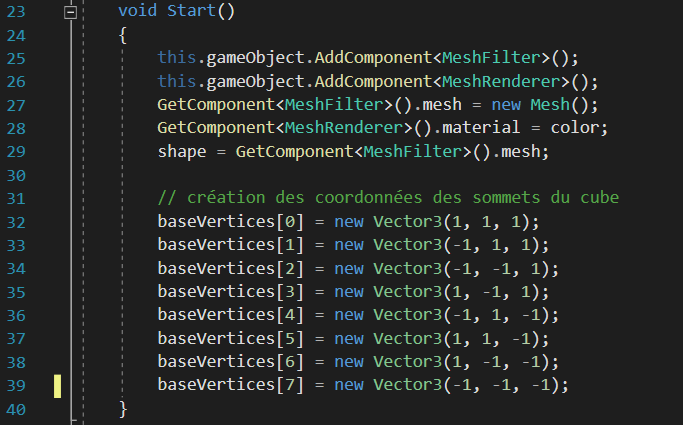
On attribue donc les coordonnées de chaque sommet du cube aux cellules de notre tableau “baseVertices”. La raison pour laquelle nous faisons cela est pour avoir les coordonnées totales des sommets du cube. Maintenant, à chaque fois que nous voudrons placer un vertex, il nous suffira de nous référer aux cellules du tableau “baseVertices”.

Remarque : Dans les coordonnées Vector3 stockées dans “baseVertices”, les écarts entre les sommets sont de 2. Nous aurions pu faire des écarts différents, mais en termes de proportion et de placement par rapport à notre “CubeGenerator”, le centre du cube sera la position exacte du GameObject.

Le problème, c’est de devoir à chaque fois calculer quelle coordonnée mettre avant laquelle ! Si vous vous souvenez bien, il faut placer les coordonnées des vertices de chaque triangle dans le sens des aiguilles d’une montre. Sachant que nous avons 24 vertices à appeler, ça fait beaucoup de travail cérébral pour pas grand chose !

Nous allons rendre un poil plus intuitif ce processus !

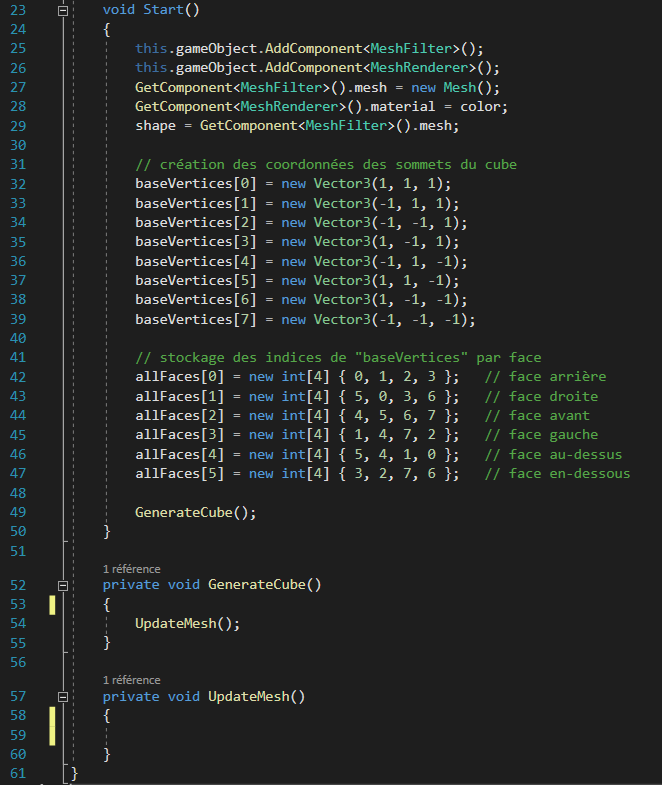
Et c’est là qu’intervient notre super tableau à deux dimensions “allFaces” !

Ce tableau va stocker, pour chaque cellules, les 4 indices qui correspondent aux coordonnées des vertices composant chaque face ! Il ne nous restera plus qu’à utiliser ces indices dans le tableau “baseVertices” et le tour est joué !

Maintenant, lorsque nous voulons avoir accès aux coordonnées des sommets de chaque faces, il nous suffit d’appeler la cellule de la face concernée dans le tableau “allFaces”, et à l’aide d’une boucle, parcourir le tableau “baseVertices” avec l’index récupéré dans “allFaces” pour avoir accès aux variables Vector3 voulues.

Le reste des opérations à mener vont se faire dans la méthode “GenerateCube()”, une fois ces dernières effectuées, nous mettrons à jour le Mesh avec la méthode “UpdateMesh()” qui sera appelée à la fin de nos opérations.

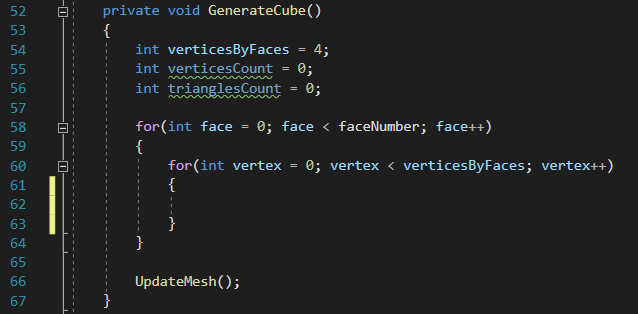
C’est ici que la partie magie va commencer !

Je vais vous expliquer ce que l’on va tenter de faire avec cette structure, et nous reviendrons sur les variables “verticesCount” et “trianglesCount” un peu plus tard.

L’idée, serait de pouvoir dire que pour chaque face de notre cube (1ere boucle “for()”), nous allons récupérer les 4 vertices qui composent cette dernière. Ces vertices seront directement enregistrés dans la variable “finalVertices” (au total 24).

La seconde partie du plan est d’enregistrer dans la foulée, les vertices propres à chaque triangle, ceux qui seront stockés dans la variable “triangles” (au total 36).

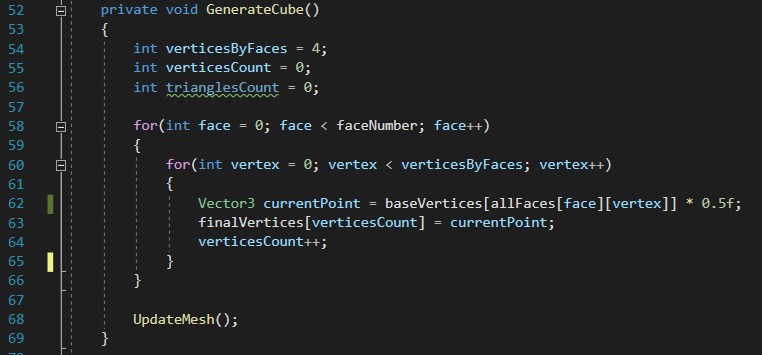
Comme vous l’aurez compris, la première boucle “for()” va se répéter 6 fois (la variable “face” étant de zéro et étant incrémentée par pas de 1 jusqu’à atteindre la valeur de la variable “faceNumber”).

Pour chaque répétition de la première boucle, nous aurons une nouvelle boucle qui elle va se réitérer 4 fois. Son but à elle, ça va être récupérer les coordonnées qui nous intéressent et de les stocker dans l’ordre des faces.
La première itération de la première boucle correspond à 0, pareil pour la seconde, donc nous enregistrons dans la variable “currentPoint” la coordonnées du premier vertex correspondant à la face arrière (voir le screenshot sur la création du tableau “allFaces”).
Nous divisons ensuite par deux le résultat récupéré (pour que notre cube est une scale de 1³) et nous injectons ce dernier dans notre tableau “finalVertices”.
Et enfin, on incrémente de 1 la variable “verticesCount”.

Remarque : L’utilité de “verticesCount” est de suivre le compte des vertices stockées. Pour que chaque cellule du tableau “finalVertices” soit remplie dans l’ordre. Donc nous pourrons avoir nos 24 vertices stockées de l’index 0 à l’index 23.

Passons aux triangles !

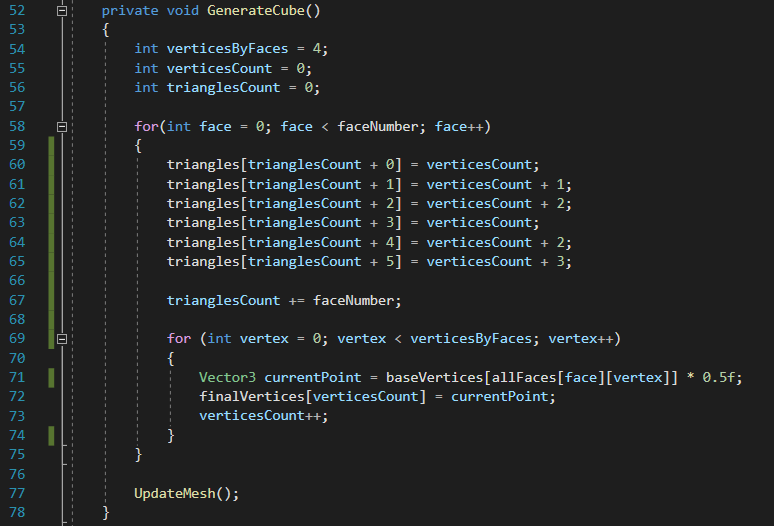
Alors cela peut paraître capillotracté, mais cela va vite prendre du sens.

Si vous avez bien suivi jusqu’ici, chaque face est composée de 2 triangles, lui-même composé de 3 vertices. Ce qui veut dire que nous avons, pour chaque face, 6 vertices à stocker dans le tableau “triangles”.
Donc pour chaque itération de la première boucle “for()”, nous allons ajouter les 6 vertices à la variable “triangles” ! Pour ce faire, nous allons récupérer la variable “trianglesCount” et la mettre en index de chaque déclaration et nous ajouterons à cet index, un int de valeur 0 à 5 pour tout enregistrer pour suivre le compte. A la fin des affectations des 6 cellules, nous incrémentons “trianglesCount” du nombre de face (6). Donc à la première itération, nous auront affecté les cellules 0 à 5 du tableau “triangles”, à la deuxième itération de la cellule 6 à 11, celle d’après de la cellule 12 à 17 jusqu’à arriver à la dernière cellule.

Nous associons à chaque cellule, l’index du vertex (celui qui est stocké dans “finalVertices”) qui compose le dit triangle. Pour ce faire, nous prenons la variable “verticesCount” (qui permet de savoir l’index de la dernière cellule remplie dans “finalVertices”) et nous lui ajoutons l’écart entre les vertices à stocker.

Par exemple : Le premier triangle sera composé des vertices 0, 1 et 2. Le second triangle sera composé des vertices 0, 2 et 3. L’écart présenté ici sera le même pour tous les triangles qui composeront la même face. Donc on garde ce même rapport avec le tableau ci-dessus.

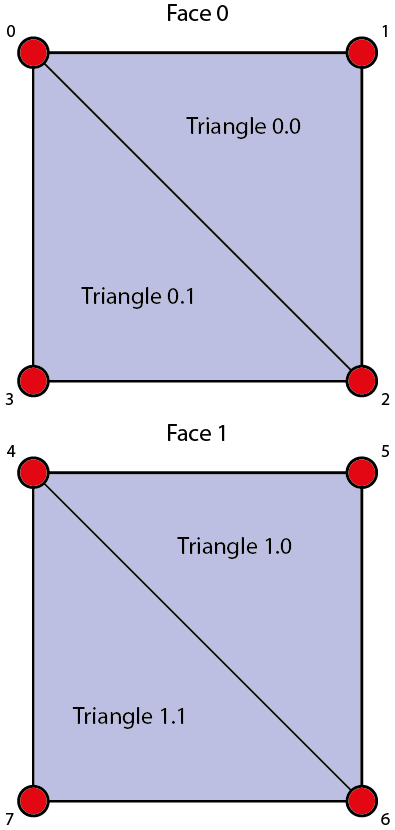
Si on se réfère à la figure ci-dessus, la variable “finalVertices” va stocker les 8 vertices visibles au-dessus. Mais la variable “triangles” va stocker les vertices correspondants, soit 12 vertices pour le total des deux triangles en exemple. Donc en résumé :
- “finalVertices” stockera (pour la figure ci-dessus) les valeurs suivantes :
{
0, 1, 2 3,
4, 5, 6, 7
}

- “triangles” stockera :
{
0, 1, 2,
0, 2, 3,
4, 5, 6,
4, 6, 7
}

Et si tout est bon de votre côté, il faut ajouter toutes ces valeurs à notre Mesh pour générer le tout !

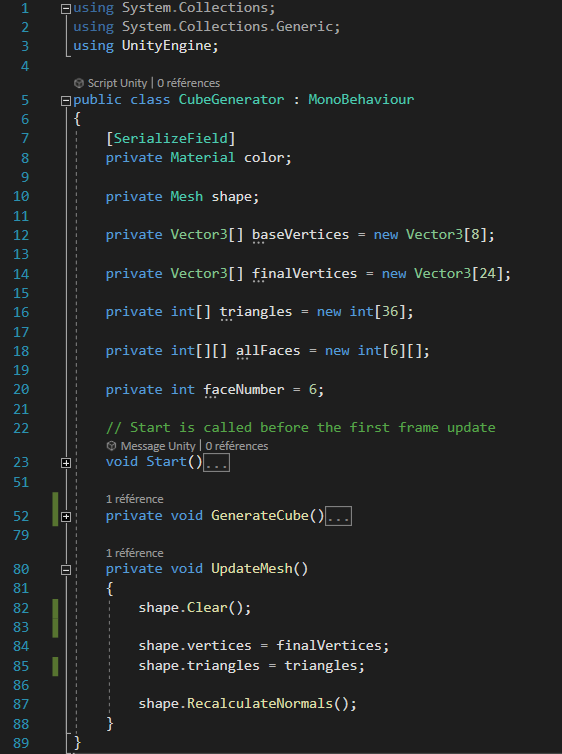
Par réflexe, il est préférable de vider le Mesh avant d’en générer un autre, donc on appelle la méthode “Clear()” de notre Mesh contenu dans la variable “shape”.

Et ensuite on attribue aux attributs “vertices” et “triangles” du Mesh, nos variables “finalVertices” et “triangles”. Grâce à ça Unity saura ce qu’il faut créer ! La méthode “RecalculateNormals()” va permettre d’avoir un comportement plus logique par rapport à nos modifications, il va rendre plus cohérent le comportement de la lumière sur le cube par exemple.

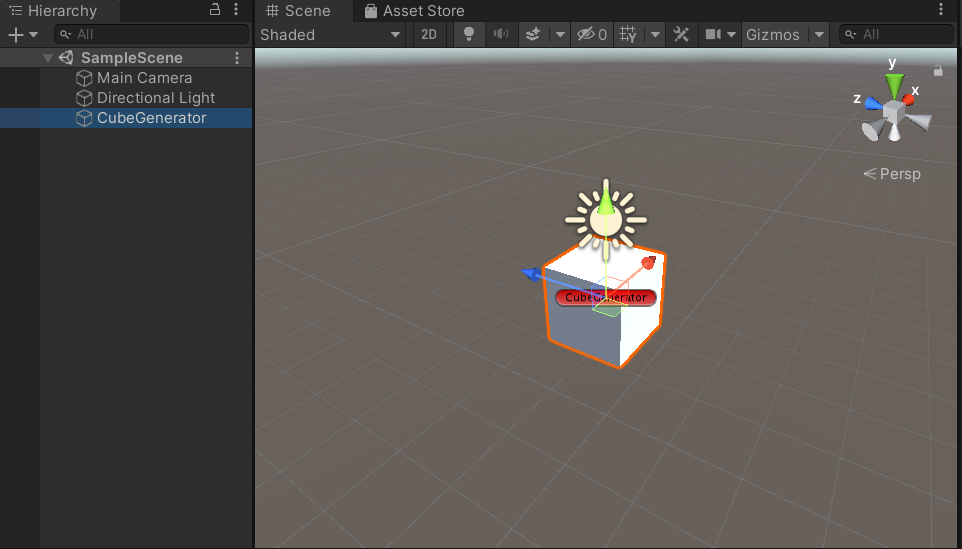
Je vous laisse retourner dans Unity, ajouter votre script à votre GameObject “CubeGenerator” et d’ajouter à ce dernier votre material (sinon rien ne s’affichera).

Admirez votre travail !